Example-1
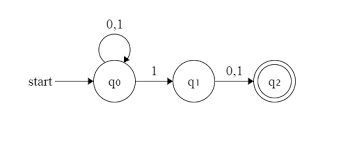
This NFA that accepts all binary strings that end with 10 and 11
In formal notation, A= {{q0,q1,q2},{0,1},δ ,q0,{q2}}
| 0 | 1 | |
|---|---|---|
| > q0 | q0q1 | q1 |
| q1 | q2 | q2 |
| * q2 | ϕ | ϕ |
In automata theory, a finite state machine is called a deterministic finite automaton (DFA), if each of its transitions is uniquely determined by its source state and input symbol, and reading an input symbol is required for each state transition.
Nondeterminism gives a machine multiple options for its moves.
In a nondeterministic finite automaton (NFA), for each state there can be zero, one, two, or more transitions corresponding to a particular symbol.
If NFA gets to state with more than one possible transition corresponding to the input symbol, we say it branches.
If NFA gets to a state where there is no valid transition, then that branch dies.
NFAs were introduced in 1959 by Michael O. Rabin and Dana Scott, who also showed their equivalence to DFAs. NFAs are used in the implementation of regular expressions: Thompson's construction is an algorithm for compiling a regular expression to an NFA that can efficiently perform pattern matching on strings.
An NFA is represented formally by a 5-tuple, A={(Q,Σ,δ ,s,F)}, consisting of
1. a finite set of states Q.
2. a finite set of input symbols σ .
3. a member of Q,s is the start state.
4. a finite set of states Q.
5. δ, the transition function is a function that takes a state in Q and an input symbol in σ as arguments and returns a subset of Q.
This NFA that accepts all binary strings that end with 10 and 11
In formal notation, A= {{q0,q1,q2},{0,1},δ ,q0,{q2}}
| 0 | 1 | |
|---|---|---|
| > q0 | q0q1 | q1 |
| q1 | q2 | q2 |
| * q2 | ϕ | ϕ |

This NFA that accepts all binary strings that end with 10 and 11
In formal notation, A= {{a,b,c},{0,1},δ ,a,{c}}
| 0 | 1 | |
|---|---|---|
| > a | ab | b |
| b | c | c |
| * c | ϕ | ϕ |

Non-deterministic finite automaton for (1/0)*001
w = F =Start state :
2.state :
3.state :
Final state:
| 0 | 1 | |
|---|---|---|
| > a | a b | a |
| b | a b c | ϕ |
| c | ϕ | a d |
| * d | ϕ | ϕ |